加权线性回归

对于 $N$ 个观测数据

\[(X_i,y_i), i=1,2,3,\cdots,N\]

可以使用线性回归模型

\[y = \beta X + \theta + \epsilon\]

来拟合 $X$ 和 $y$ 之间的关系。其中的参数 $\beta,\theta$ 通常使用最小二乘拟合，即按照使代价函数

\[J(\beta,\theta) = \frac{1}{N} \sum_{i=1}^N (y_i - \beta X_i - \theta)^2\]

最小的 $\hat \beta,\hat \theta$，使得拟合曲线尽可能地接近所有的观测点，这就是一般的线性回归。

加权线性回归

但在实际应用中，观测点之间可能是由差异的。比如，有的观测点误差大，有的观测点误差小，这就需要让拟合直线 $y = \beta X + \theta$ 优先拟合误差较小的观测点。这时我们就可以使用一个权重系数 $w_i$ 来表示第 $i$ 个观测点的权重 (例如，对于误差小的观测点，$w_i$ 的值更大) 考虑了这个权重系数的 $w_i$ 的线性回归，就是加权线性回归。

它的回归方差仍然是 $y = \beta X + \theta + \epsilon$，唯一的区别是代价函数变成了

\[J(\beta,\theta) = \frac{1}{N} \sum_{i=1}^N w_i (y_i - \beta X_i - \theta)^2\]

这样，我们在寻找最优 $\beta,\theta$ 时，就可以更多地考虑高权重的观测值。

参数求解

这里以一个自变量 $x_i$ 理解求解过程为例:

\[\hat \beta, \hat \theta = arg\min_{\hat \beta,\hat \theta} J(\beta,\theta)\]

$J$ 的值一定是大于 0 的，且只有一个极值点，定然为最小值，所以可以采用求偏导的方式求极值点所在位置：

\[\frac{\partial J}{\partial \beta} = 0 \\ \frac{\partial J}{\partial \theta} = 0\]

求解过程不复杂，最终结果如下：

\[\hat \beta = \frac{\sum_i^N w_i x_i y_i - \frac{\sum_i^N w_i y_i \cdot \sum_i^N w_i x_i}{\sum_i^N w_i}} {\sum_i^N w_i x_i^2 - \frac{(\sum_i^N w_i x_i)^2}{\sum_i^N w_i}} \\ \hat \theta = \frac{\sum_i^N w_i y_i - \hat \beta \sum_i^N w_i x_i} {\sum_i^N w_i}\]

Note: 这里可以用其它符号替代，但这样写在一起更能理解线性回归参数和数据的关系。

大部分博客对加权线性回归的重点关注参数估计，对加权影响参数检验的关注不够。权重代表数据点的重要性，在加权凸显部分数据的重要性时，这也会影响后续的参数显著性检验。我在实际应用（以lm()为例）分析数据的过程，发现加权可能导致假阳性，或者使参数检验的结果偏保守。

两个影响显著性检验的加权案例

1. ‘比例’ 回归

场景：自变量服从独立同正态分布 $(x_1,x_2,\cdots,x_n)$，因变量也服从独立同正态分布 $(y_1,y_2,\cdots,y_n)$，还有一组观测数据 $(u_1,u_2,\cdots,u_n)$ （非随机变量，确定值），需要对 $y_i/ u_i$ 和 $x_i/u_i$ 进行线性回归，并对斜率进行统计检验。

模拟零假设：模拟 $y_i = 0\cdot x_i + \epsilon_i$，因此理论上 $y_i / u_i$ 和 $x_i / u_i$ 也不相关。

结果比较：比较不同权重模型，包括

• model 1:一般线性回归；
• model 2: 各数据点权重为 $\lvert u_i\rvert$；
• model 3: 各数据点权重为 $u_i^2$。

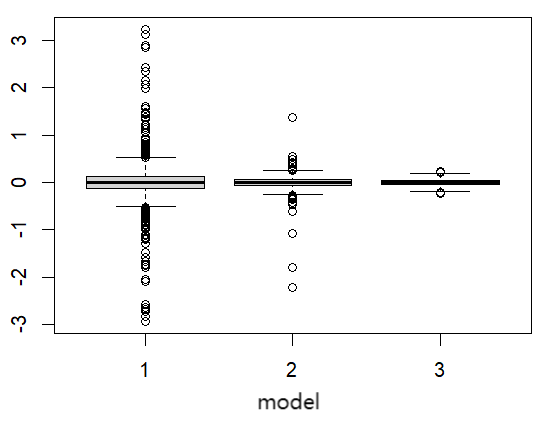
斜率：

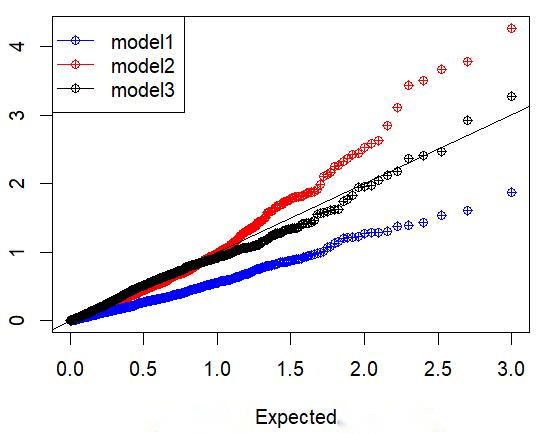
斜率对应的P值 Q-Q 图：

模拟代码：

set.seed(0)
Data1 = data.frame(theta = seq(1000),beta = seq(1000),P_beta=seq(1000))
Data2 =data.frame(theta = seq(1000),beta = seq(1000),P_beta=seq(1000))
Data3 = data.frame(theta = seq(1000),beta = seq(1000),P_beta=seq(1000))
    
for(i in seq(1000)){
    gamma = 0
    X = rnorm(200)
    Y = gamma * X + rnorm(200)
    U = abs(rnorm(200,3,1))
    
    Y_U = Y/U
    X_U = X/U
    
    model1 = summary(lm(Y_U~X_U))   
    model2 = summary(lm(Y_U~X_U,weights = U))   
    model3 = summary(lm(Y_U~X_U,weights = U^2))   
    
    Data1[i,] = c(model1$coefficients[,"Estimate"],model1$coefficients["X_U","Pr(>|t|)"])
    Data2[i,] = c(model2$coefficients[,"Estimate"],model2$coefficients["X_U","Pr(>|t|)"])
    Data3[i,] = c(model3$coefficients[,"Estimate"],model3$coefficients["X_U","Pr(>|t|)"])
}

boxplot(Data1$beta,Data2$beta,Data3$beta)

Expected = sort(-log10(seq(1000)/1000))
plot(c(Expected,Expected,Expected),
     c(sort(-log10(Data1$P_beta)),sort(-log10(Data2$P_beta)),sort(-log10(Data3$P_beta))),
     col = c(rep("red",1000),rep("blue",1000),rep("black",1000)),
     pch=10)
legend("topleft", # 图例位置
       legend = c("model1", "model2", "model3"), # 图例名称
       col = c("blue", "red","black"), # 颜色
       pch = c(10, 10,10), # 点样式
       lty = c(1, 1)) # 线型
abline(b=1,a=0)

2. 随机因变量和自变量

场景：观测数据可能是对某个真实场景的估计结果，比如 $N$ 个观测数据 $(\hat x_i,\hat y_i)$，每个观察数据都来自于不同的正态分布，即 \(\hat x_i \sim N(x_i,\sigma^2_{xi}),\hat y_i \sim N(y_i,\sigma^2_{yi}),i =1,2,\cdots,N\)

需要对 $\hat y_i$ 和 $\hat x_i$ 进行线性回归，并对斜率进行统计检验。

模拟零假设：模拟 $y_i = 0\cdot x_i + \epsilon_i$

结果比较：比较不同权重模型，包括

• model 1:一般线性回归；
• model 2: 各数据点权重为 $\lvert \sigma_{yi}\rvert ^{-1}$；
• model 3: 各数据点权重为 $\sigma_{yi}^{-2}$。

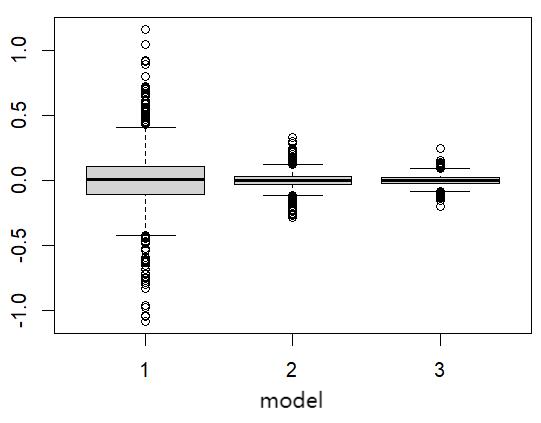
斜率：

斜率对应的P值 Q-Q 图：

模拟代码：

Note: 这里模拟的是20个样本量，200个样本量似乎样本量足够，不同模型没有区别。

set.seed(0)
Data1 = data.frame(theta = seq(1000),beta = seq(1000),P_beta=seq(1000))
Data2 =data.frame(theta = seq(1000),beta = seq(1000),P_beta=seq(1000))
Data3 = data.frame(theta = seq(1000),beta = seq(1000),P_beta=seq(1000))

N = 20 # 200
for(i in seq(1000)){
    gamma = 0
    X_mean = rnorm(N)
    sd_X = rchisq(N,1) + 0.1
    X = rnorm(N,X_mean,sd_X)
    
    mean_Y = gamma * X_mean
    sd_Y = rchisq(N,1) + 0.1
    Y = mean_Y + rnorm(N,0,sd_Y)
    
    model1 = summary(lm(Y~X))
    model2 = summary(lm(Y~X,weights = abs(sd_Y)^-1))   
    model3 = summary(lm(Y~X,weights = sd_Y^-2))   
    
    Data1[i,] = c(model1$coefficients[,"Estimate"],model1$coefficients["X","Pr(>|t|)"])
    Data2[i,] = c(model2$coefficients[,"Estimate"],model2$coefficients["X","Pr(>|t|)"])
    Data3[i,] = c(model3$coefficients[,"Estimate"],model3$coefficients["X","Pr(>|t|)"])
}

boxplot(Data1$beta,Data2$beta,Data3$beta)

Expected = sort(-log10(seq(1000)/1000))
plot(c(Expected,Expected,Expected),
     c(sort(-log10(Data1$P_beta)),sort(-log10(Data2$P_beta)),sort(-log10(Data3$P_beta))),
     col = c(rep("red",1000),rep("blue",1000),rep("black",1000)),
     pch=10)
legend("topleft", # 图例位置
       legend = c("model1", "model2", "model3"), # 图例名称
       col = c("blue", "red","black"), # 颜色
       pch = c(10, 10,10), # 点样式
       lty = c(1, 1)) # 线型
abline(b=1,a=0)

3 案例总结

在这两个例子中，是否加权不会使结果产生偏差，加权的作用是优先可靠的数据点，这可以让估计的结果更稳定，方差更小。但加权会影响参数的统计检验，在案例1——比例回归中，不加权会是参数检验的P值产生假阳性，并且假阳性比例非常高；在案例2——随机因变量和自变量中，不加权会使推断结果偏保守，错误的权重又会让结果产生假阳性。这两个案例体现了加权对参数检验的影响，虽然加权考虑数据的重要性，使估计结果更稳定，但加权对统计检验的影响也不容忽视，错误的权重选择会使统计检验的结果失效，影响后续的分析。如何构造可以保证统计检验有效的加权非常重要。

如何有效加权？

加权线性回归有效性的证明有几个方面：

• 参数的分布是正态分布；
• 参数估计是无偏的；
• lm()中正态分布的方差计算正确 (问题关键)；

1. 参数估计服从正态分布

在一般线性回归中，我们一般将自变量看作固定的，只考虑因变量的随机性，即使是加权线性回归也是如此。在上面 $(\hat \beta,\hat \theta)$ 的估计表达式中，都是对 $y_i$ 的线性组合，而 $y_i$ 是正态分布（正态性假设），因此 $(\hat \beta,\hat \theta)$ 也都是服从正态分布。

2. 参数估计是无偏的

证明无偏估计，即验证均值$E(\hat \beta) = \beta$，这里我们以 $\hat \beta$ 为例：

\[E(\hat \beta) = E(\frac{\sum_i^N w_i x_i y_i - \frac{\sum_i^N w_i y_i \cdot \sum_i^N w_i x_i}{\sum_i^N w_i}} {\sum_i^N w_i x_i^2 - \frac{(\sum_i^N w_i x_i)^2}{\sum_i^N w_i}}) \\ = E( \frac{\sum_i^N w_i x_i (\beta X_i + \theta) - \frac{\sum_i^N w_i (\beta X_i + \theta) \cdot \sum_i^N w_i x_i}{\sum_i^N w_i}} {\sum_i^N w_i x_i^2 - \frac{(\sum_i^N w_i x_i)^2}{\sum_i^N w_i}}) \\ = \beta\]

3. 正态分布的方差计算正确 (问题关键)

加权线性回归的方差计算：

要进行统计推断还有最重要的一步，计算方差 $var(\hat \beta)$: \(Var(\hat \beta) = Var(\frac{\sum_i^N w_i x_i y_i - \frac{\sum_i^N w_i y_i \cdot \sum_i^N w_i x_i}{\sum_i^N w_i}} {\sum_i^N w_i x_i^2 - \frac{(\sum_i^N w_i x_i)^2}{\sum_i^N w_i}}) \\ = Var(\frac{\sum_i^N w_i \cdot \sum_i^N w_i x_i y_i - \sum_i^N w_i y_i \cdot \sum_i^N w_i x_i} {\sum_i^N w_i\cdot \sum_i^N w_i x_i^2 - (\sum_i^N w_i x_i)^2})\)

这里公式实在太多了，我把 $\sum_i^N w_i$ 和 $\sum_i^N w_i x_i$ 分别简写为 $\overline w$ 和 $\overline {wx}$、分母 $\sum_i^N w_i\cdot \sum_i^N w_i x_i^2 - (\sum_i^N w_i x_i)^2$ 简写为 $D$:

\[Var(\hat \beta) = Var(\frac{\overline w \cdot \sum_i^N w_i x_i y_i - \sum_i^N w_i y_i \cdot \overline {wx}}{D}) \\ = Var(\frac{\sum_i^N (\overline w x_i - \overline {wx}) w_i\epsilon_i }{D})\]

$\epsilon_i$ 是服从均值为零的正态分布，如果每个都已知，方差可以很容易地估计出来，但它的分布是未知的。一般的线性回归会假设 $\epsilon_i$ 服从独立同分布，在加权线性回归中也是类似，也要假设独立同分布，但有一点不一样。这个不同点要从加权线性回归的拟合函数说起，(加权)最小二乘 $\sum_{i=1}^N w_i (y_i - \beta X_i - \theta)^2$​ 在统计分析中的意义是不可解释的残差最小，因此

\(\sigma_i^2 = w_i (y_i - \beta X_i - \theta)^2 = (\sqrt w_i \epsilon_i)^2\) 加权线性回归中假设的是 $\sqrt w_i \epsilon_i$ 的方差相同，服从独立同分布。在这个假设下，我没才能计算得到 $\hat \beta$ 的方差： \(Var(\hat \beta) = Var(\frac{\sum_i^N (\overline w x_i - \overline {wx}) w_i\epsilon_i }{D}) \\ = \frac{\sum_i^N ((\overline w x_i - \overline {wx}) \sqrt{w_i} )^2}{D^2} var(\sqrt{w_i}\epsilon_i) \\ = \frac{\sum_i^N (\overline w x_i - \overline {wx})^2 w_i }{D^2} \cdot Se\)

其中 $Se = \frac{\sum_i w_i (y_i - \beta X_i - \theta)^2}{N-2}$。

4. 总结

在 1-3 点的推到中可以看出，加权让统计检验失效的原因使加权后，违背了加权线性回归中的独立同分布特点。例如：

• 在第一个例子中，虽然随机变量 $y_i$ 服从独立同正态分布，但 $y_i/u_i$ 则不再是服从相同的分布了，使用普通的线性回归自然会产生偏差。而考虑了加权线性回归，使用 $w_i = u_i^2$ 进行加权，此时加权后的方差相同，即 $w_i \cdot var(y_i/u_i) = w_j \cdot var(y_j/u_j), i\ne j$ ，满足加权线性回归的同分布条件，因此有效。
• 第二个例子也和第一个例子类似，使用方差倒数进行加权可以是加权线性回归满足同分布条件。

想让 lm() 保证统计检验有效，可以通过确保加权后的残差分布相同（ $w_i \cdot var(y_i/u_i) = w_j \cdot var(y_j/u_j), i\ne j$）来选择确定权重。

实际上，R包中的lm()这类函数只是加权线性回归的通用形式，在正态分布下，即使完全不加权或者随意加权，估计的参数也是服从正态分布，只是与lm() 对方差的特定计算不符合。我们完全可以自己推导相关的方差进行统计分析，特别是在一些非线性加权（比如权重会随着 $y_i$ 大小变化而变化），这种自己推导将非常有效。

这里的证明论述也有一点需要注意：在验证线性回归的参数服从正态分布时，更一般的证明是使用中心极限定理证明，它还可以用来证明因变量不服从正态分布的广义线性回归，估计参数依然服从正态分布。前提是有足够的样本量。在我们的第二个例子，样本量较大（>200）,不加权的方法也有效，但样本量只有20时就会存在偏差。第一个例子可能就必须使用加权了，因为$Y/U$分布是随着样本变化而变化。当将 $U$ 固定在一定范围，当样本量越来越大时，最终不加权也会有效。

Reference

这个加权线性回归的原理推到是基于机器学习：https://xg1990.com/blog/archives/164

关于统计分析的问题参考了StackExchange上的一篇问答篇：https://stats.stackexchange.com/questions/138938/correct-standard-errors-for-weighted-linear-regression